

| Accueil | Commandes | Pièce perdue ? | ||
| Histoire | Indices | Sites amis | ||
| Références | Solutions | Défis ! | ||
 Le Gnomon de Zhou (Liu Hui vers 263 AD) est la toute première démonstration géométrique par dissection connue du théorème de Pythagore (désigné alors sous le nom de théorème de Gougu). Thabit Ibn Qurra' (826 - 901) et Bhaskara Acharya (1114 - 1185), ont tous deux proposé de très célèbres preuves géométriques par dissection. Si nous pouvions leur demander comment découper un carré en trois carrés identiques, ils nous répondraient très probablement : “Utilisez ma dissection pour diviser le carré en deux carrés de surface 1/3 et 2/3, puis découpez simplement le carré de surface 2/3 en deux !”. Ces preuves du théorème de Pythagore par dissection donnent des solutions valides mais non minimales. 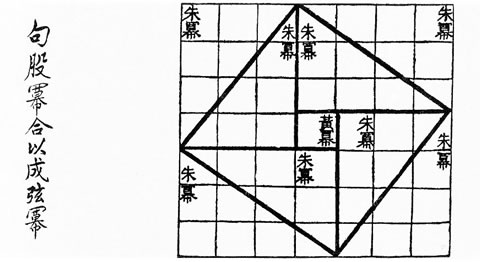
Gnomon de Zhou (Liu Hui vers 263 AD) Du VIIIème sciècle au XVème sciècle, le peuple Musulman rayonnait intellectuellement sur le monde par ses sciences (voir l'Encyclopédie de l'Histoire des Sciences Arabes par Roshdi Rashed (1996), Vol. 2 Chap. 14, par B.A. Rosenfeld et A.P. Youschkevitch). A cette époque, les mosquées érigées à la gloire d'Allah, recevaient un décor uniquement non-figuratif afin d'empêcher que l'esprit ne soit détourné du vide contemplatif. Les artisans les ornaient à l'aide de mosaïques aux motifs géométriques d'une grande valeur esthétique et se retrouvaient parfois face à des problèmes de découpage géométrique complexes. Un de ces problèmes était comment assembler trois carrés pour en faire un plus grand. Muhammad ibn Muhammad ibn Yahya ibn Isma'il ibn al-'Abbas Abu'l-Wafa' al-Buzajani (940 - 998), célèbre mathématicien et astronome Iranien, publia dans l'ouvrage intitulé "Kitâb fîmâ yahtâju ilayhi al-sâni` min a`mâl al-handasa" qui signifie "Constructions géométriques à l'usage des artisans" (chapitre sur comment diviser et assembler un carré), la première solution à neuf morceaux connue pour ce problème. Un de ses manuscrits nous est parvenu et est visible à la BNF (Bibliothèque Nationale Française) de Paris. Dans ce traité, il écrit : “J'étais présent à une réunion à laquelle un grand nombre de géomètres et d'artisans participaient. On leur avait demandé de construire un carré à partir de trois carrés égaux. Les géomètres pouvaient aisément construire une ligne telle que son carré était égale à la surface des trois carrés, mais aucun des artisans n'était satisfait. Ils souhaitaient diviser ces carrés en morceaux pouvant être réassemblés en un grand carré. [...] Certains artisans positionnaient un des carrés au milieu, divisaient le second par la diagonale et divisaient le troisième carré en un triangle rectangle isocèle et deux trapezoïdes congruents qu'ils assemblaient ensemble.” 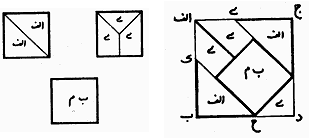
Une "solution" fausse ! (crédit Reza Sarhangi) Si nous supposons que le petit carré central a une longueur unité, alors les diagonales du grand carré final doivent être égales à 1 + racine_carrée(2), ce qui est plus petit que racine_carrée(6), la diagonale du carré d'aire trois. Ainsi cette construction est fausse. Abu'l-Wafa' généralisa sa dissection pour proposer une nouvelle démonstration géométrique du théorème de Pythagore (cf. Alpay Özdural). C'est la représentation de cette généralisation qui est visible en mosaïque sur la Jameh Mosque d'Isfahan (figure ci-dessous). 
Mosquée du Vendredi à Isfahan Vers les années 1300, une nouvelle solution en neuf pièces et une solution en 8 pièces furent trouvées, probablement par Abu Bakr al-Khalil al-Tajir al-Rasadi. Il a fallut attendre le 18 ème - 19 ème siècle pour Jean-Étienne Montucla, Jacques Ozanam, Philip Kelland, Paul Busschop, Le Colonnel De Coatpont, Edouard Lucas proposent d'autres solutions en huit ou sept pièces. Mais c'est très probablement vers 1830 - 1840 qu'Henry Perigal trouve la première solution utilisant six pièces (voir une note bibliographique sur H. Perial en appendice d'une publication de Rogers en 1897). Sa solution est très similaire à la dissection du gnomon (un carré avec un coin en moins qui forme un "L") proposée par P. Kelland et publiée en 1955. H. Perigal ne publia sa technique pour transformer un rectangle en carré qu'en 1875 et sa technique appliquée à trois carrés congruents qu'en 1891. Notons que sa solution est très similaire à celle proposée par Abu Bakrs al-Khalil 500 ans plutôt. La version de H. Perigal est asymétrique mais, en faisant glisser la diagonale de la coupe, élimine deux pièces par rapport à celle d'Abu Bakrs al-Khalil. Henry Perigal a également redécouvert la dissection d'Abu'l-Wafa' pour démontrer le théorème de Pythagore. Il considéra ce résultat comme sa plus belle preuve. Elle est aujourd'hui gravée sur sa tombe. 

Tombe d'Henry Perigal Durant le XX ème siècle, Henry Ernest Dudeney et Sam Loyd's republièrent la solution de Perigal. D'autres solutions inédites, avec plus de pièces sont encore trouvées. Au XXI ème siècle, Greg N. Frederickson proposa une solution en sept pièces qui pave le plan par translation et Nobuyuki Yoshigahara une dissection en neuf pièces qui utilise exactement trois fois la même dissection pour les trois carrés de départ (solution qui pourrait en fait être ramenée à sept pièces). En 2010, Christian Blanvillain et János Pach proposent une famille de solutions symétriques en six pièces non convexes. Greg N. Frederickson fait remarquer que pour une position donnée particulière, toutes les 6 pièces ont exactement la même surface ! Ce qui rend cette dissection vraiment unique. Le Quadratum Cubicum est composé de neuf de ces solutions, sélectionnées pour leur esthétique et leur importance historique. Pour plus d'informations sur la fabuleuse histoire de ce problème, nous vous renvoyons aux liens bibliographiques en référence et aux trois excellents livres du Professeur Greg N. Frederickson qui regorgent de bien d'autres trésors ! |
||
| Accueil | Commandes | Piece perdue ? | ||
| Histoire | Indices | Sites amis | ||
| Références | Solutions | Défis ! | ||